What controls the entrainment rate of dry buoyant thermals?
Submitter
Morrison, Hugh Clifton — University Corporation for Atmospheric Research
Area of research
Vertical Velocity
Journal Reference
Science
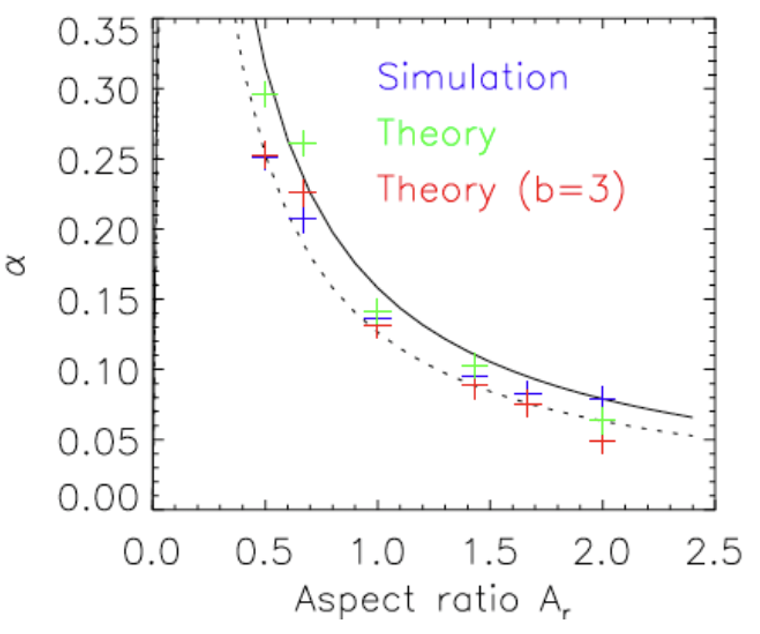
Thermals, or rising bubbles of buoyant air, are a key component of atmospheric flows. It is well known that thermals initially at rest expand as they rise. In idealized conditions with initially spherical thermals starting from rest, the thermal radius expands about 15% of the distance the thermal rises. The goals of this study were to: 1) explain why thermals expand at this particular rate as they rise; and 2) explain why initially flat thermals (width greater than height) expand more than initially spherical thermals.
Impact
This study showed that a simple theoretical model of thermal expansion could well reproduce results from numerical simulations. The reason why the thermal radius expands at 15% of the distance it rises is related to the timescale for fluid in the thermal’s core to be swept away by entrainment. This work is relevant to buoyantly driven atmospheric flows, especially those with a localized pulse source of buoyancy or steady source that leads to a chain of multiple thermals. Spreading rates of dry thermals may also indirectly impact cumulus entrainment rates by influencing the size of thermals at cloud base.
Summary
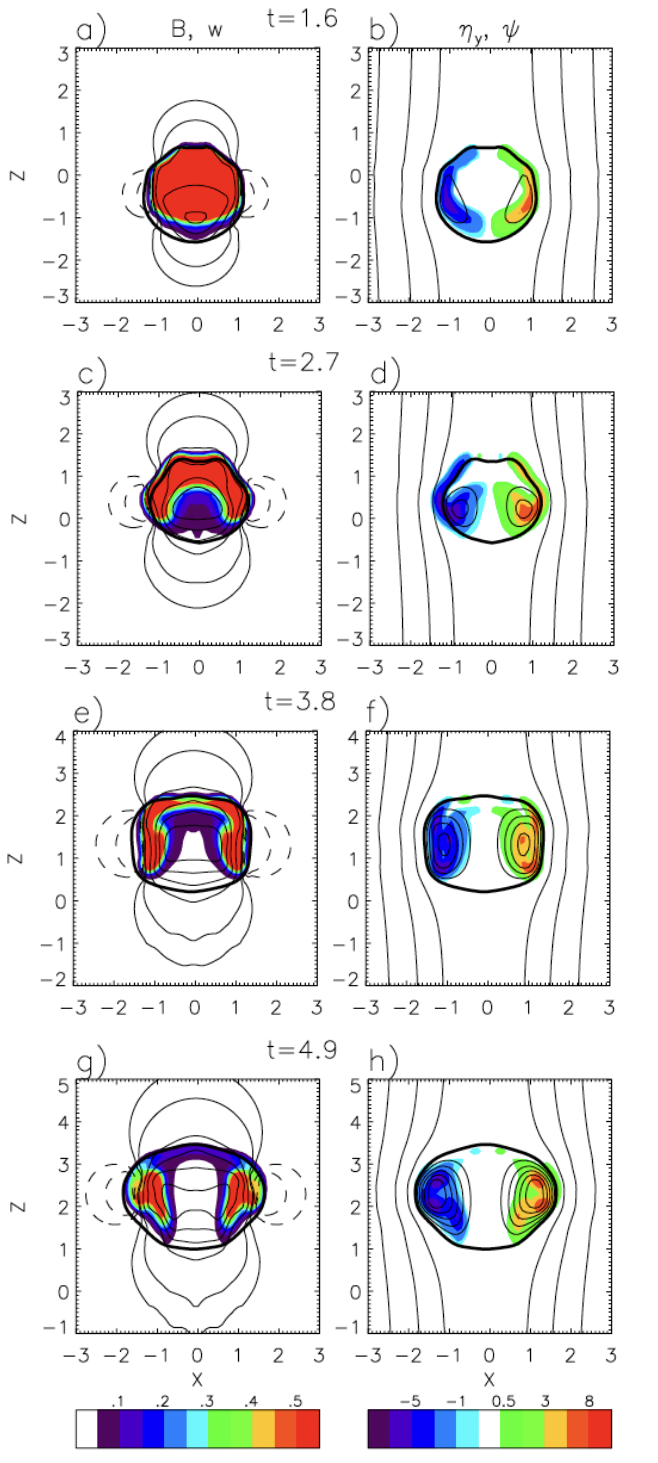
An analytic model for the ascent rate of thermals as a function of their expansion (entrainment) rate was derived from the thermal-averaged vertical momentum budget equation. From this equation, a critical height was defined as the height where the thermal’s ascent rate peaks, which is linearly related to the expansion rate. The critical height is also the height of thermal top when the fluid in the thermal core is swept out from entrainment. The timescale for this sweeping out process is controlled by the vertical velocity of a parcel ascending through the thermal core, relative to the ascent rate of the thermal as a whole. A theoretical model for the parcel velocity was derived by approximating the internal flow of the thermal using a simple mathematical model called Hill’s vortex. Combined with the analytic equation for thermal ascent rate, a simple expression for the expansion rate as a function of the initial thermal aspect ratio (height divided by width) was obtained. The expansion rate from this simple theoretical expression well matched the expansion rate directly calculated from a set of numerical simulations, including the 15% rate for initially spherical thermals. Overall, this study provides a theoretical underpinning for understanding the entrainment behavior of thermals, and in particular has elucidated the factors controlling the spreading rate of thermals.
Figure 1. Non-dimensional thermal radius expansion rate alpha (y-axis) as a function of the initial thermal aspect ratio Ar (height divided by width) (x-axis). Values directly calculated from the numerical simulations are indicated by blue crosses, and theoretical values with different assumptions are shown by the green and red crosses as well as the solid and dotted lines. The solid line is the theoretical relation alpha = (31/4 - 1)/(2Ar). From journal.
Figure 2. Vertical cross-section plots at different times (t) for a numerically simulated rising thermal. Left column: non-dimensional buoyancy (color contours) and vertical velocity (contour lines). Right column: vorticity in the y-plane (color contours) and stream function (contour lines). Thick solid lines in all plots indicate the thermal boundary. As the thermal rises, non-buoyant environmental fluid sweeps into the thermal core from below as seen moving from top to bottom in the left column. The timescale for this process controls the thermal expansion rate. From journal.